
읽어주셔서 감사합니다. 오늘은 백준의 1002번, 터렛 문제에 대해 풀어보도록 하겠습니다.
코드
아래 내용은 수학적인 내용을 다량 함유하고 있습니다. 사실상 수학적인 내용을 제외하면 일반적인 초보자가 짤 수 있는 수준의 코드이지요. 수학적 내용은 아래에서 설명하겠습니다.
#include <iostream>
#include <cmath>
using namespace std;
#define square(x) ((x)*(x))
int main(void) {
int r1, r2;
int x1, y1, x2, y2;
double D;
int T;
cin >> T;
for (int i = 0; i < T; i++) {
cin >> x1 >> y1 >> r1 >> x2 >> y2 >> r2;
D = sqrt(square(x1 - x2) + square(y1 - y2));
if ((r1 == r2) && (x1 == x2) && (y1 == y2))
cout << -1;
else if ((abs(r1 - r2) < D) && (D < r1 + r2))
cout << 2;
else if ((r1 + r2 == D) || (abs(r1 - r2) == D))
cout << 1;
else
cout << 0;
cout << endl;
}
return 0;
}수학적 내용
먼저 우리가 풀 문제를 간략화 시킬 필요가있다.
(x1, y1)에 존재하는 조규현의 입장에서는, 류재명이 자신과 거리가 r1만큼 떨어져 있는 모든 지점 즉 (x1, y1)이 중심이고, 반지름이 r1인 원 위에 존재해야 한다는 것을 알 수 있고, 마찬가지로, 백승환의 입장에서는 류재명이 (x2, y2)가 중심이고, 반지름이 r2인 원 위에 존재해야 한다는 것을 알 수 있다.
이 둘의 정보를 모두 조합하게 되면, 결국 두 원의 교점이 류재명이 존재할 수 있는 위치가 된다.
즉, 이 문제는 (x1, y1)이 중심인 반지름이 r1인 원과, 중심이 (x2, y2)인 반지름이 r2인 원과의 교점의 개수를 구하는 문제이다.
이제 각 상황에 맞춰 조건을 계산해보자. 아래 계산된 식들은 모두 프로그램 코드의 else if, if문에 작성되어있다.
1) 두 원의 교점이 무한개이다.
이 경우는 자명하게도(당연하게도) x1과 x2, y1과 y2, r1과 r2가 모두 같은 경우이다. 두 원이 동일한 경우이기 떄문
2) 두 원의 교점이 1개이다.
이 경우, 두 점간의 거리 D와 각 원의 반지름 r1, r2는 다음 두 경우중 한 경우를 만족해야 한다.
r1 + r2 = D 또는 |r1 - r2| = D (|x|는 x의 절댓값)
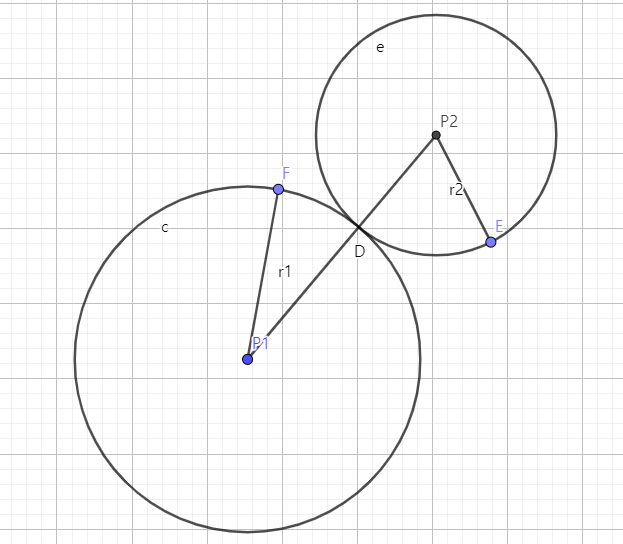
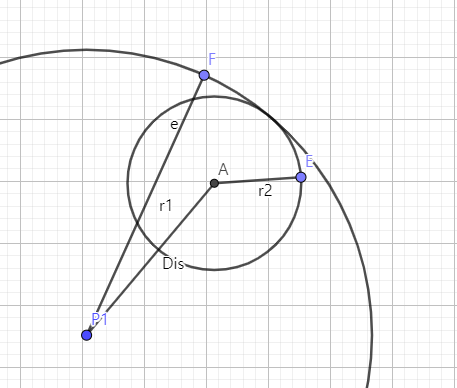
3) 두 원의 교점이 2개이다.
이 경우 교점이 1개일때의 조건을 응용하여 아래와 같이 조건을 설정할 수 있다.
마찬가지로 두 점 간의 거리를 D라 설정하였다.
|r1 - r2| < D < r1 + r2
4) 두 원의 교점이 0개이다.
마찬가지로 교점이 1개일떄의 조선을 응용해 나타낼 수 있다.
두 점간의 저리를 D라 설정하였다.
D < |r1 - r2| or D > r1 + r2
이 조건은 위 수식처럼 표현 될 수도 있으나, 프로그래밍에서는 else문으로 처리될 수도 있다.
사용방법
백준 1002번 참고
https://www.acmicpc.net/problem/1002
1002번: 터렛
각 테스트 케이스마다 류재명이 있을 수 있는 위치의 수를 출력한다. 만약 류재명이 있을 수 있는 위치의 개수가 무한대일 경우에는 -1을 출력한다.
www.acmicpc.net
실행화면
프로그램의 사용 목적을 고려하여 실행화면은 생략하도록 하겠습니다.
'C C++ language' 카테고리의 다른 글
| C++ 어린 왕자 문제 풀기 (백준 1004) (0) | 2021.06.12 |
|---|---|
| C++ 피보나치 함수 문제 풀기 (백준 1003) (0) | 2021.06.05 |
| C언어 두 정수 입력수 빼서 출력하기 (백준 1001) (0) | 2021.05.22 |
| C언어 두 정수 입력 후 더하여 출력하기 (0) | 2021.05.15 |
| C언어 배열의 순서 바꿔서 출력하기 (with source) (0) | 2021.05.08 |



